I'm loss'd
this post was submitted on 22 Jul 2024
551 points (93.2% liked)
Science Memes
10905 readers
1007 users here now
Welcome to c/science_memes @ Mander.xyz!
A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.
Rules
- Don't throw mud. Behave like an intellectual and remember the human.
- Keep it rooted (on topic).
- No spam.
- Infographics welcome, get schooled.
This is a science community. We use the Dawkins definition of meme.
Research Committee
Other Mander Communities
Science and Research
Biology and Life Sciences
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- !reptiles and [email protected]
Physical Sciences
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
- [email protected]
Humanities and Social Sciences
Practical and Applied Sciences
- !exercise-and [email protected]
- [email protected]
- !self [email protected]
- [email protected]
- [email protected]
- [email protected]
Memes
Miscellaneous
founded 2 years ago
MODERATORS
L
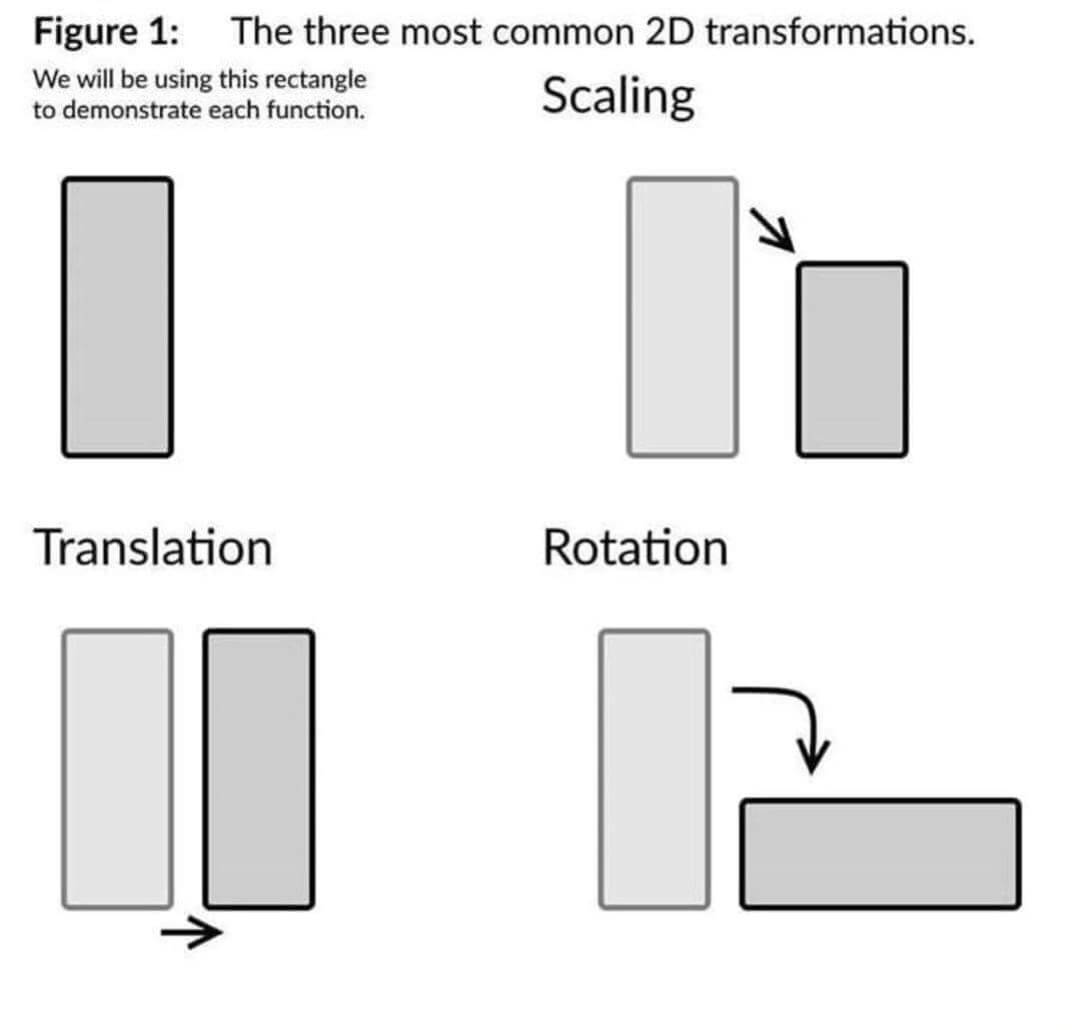
The second is not really scaled, and the second and forth have translation. Usually that wouldn't be a problem for demonstrative proposed, if translation wouldn't be shown explicitly. Can be fixed by introducing a canvas of the before/after picture
The second is scaled in one axis, and had translation otherwise it would be hard to understand. And the rotation can be achieved by moving the origin of rotation.
Ffs
Don't use this. It's not a lossless transformation!
Meanwhile, in SVG: <g filter="scale: 0.5"><xlink:use … /></g>
Um
The second wrong.
Or...only one
Dimension
I don’t get it.
Only the transformations one is correct. All the other ones seemingly also preform a translation, and even if they might be correct if you take the orgin to be slightly outside of the shape but that's bad for educational purposes. Also this one makes the translation transformation look like the identity transformation.
This last one might just be me, but shouldn't shearing be included here?
You don't get it either
Could you explain it then?
It’s a “loss” meme.
Me too, I'm at a loss.
What is “loss” in this context?
Know Your Meme's page on Loss.
Basically, a 2000s webcomic about gamer culture devoted a comic (titled Loss) to the writer's partner who had a miscarriage. It's four wordless panels, and the characters in each panel take up roughly the positions of the rectangles in the OP.
Tonally, it was the complete opposite of what the webcomic normally covered, and it really shocked its readers who, being an internet community, responded with irony and parody, and now there are a ton of Loss references out there.
Thank you.
Ok ... I didn't know this meme (too old and/or out of the loop I suppose) ... so out of annoyance I looked it up ...
... and yea ... as far as trolling is concerned gotta pay the game here ... not sure it was worth 15 mins of my life but ... kudos I guess
Oh no, not The Game!
😏
I had to look at this twice to get it. I must be losing my touch.
Goddammit. This is like getting rickrolled.
dQw4
w9Wg
> Goddamnit.
> This is
> like getting
> rick[rolling something involves flattening it]
We rarely get rickrolled anymore, such a loss
Is this science?
...seriously, I'm at a loss
We like to do a little trolling
No shear is disappointing.
Yeah, such a big loss it wasn't included.
Scaling looks like scaling+translation? And rotation looks like either rotation+translation, or scaling+translation?
That's because it's loss
Oooh🤦♂️
I'm at a loss here.
Son of a bitch, stole my line
You sly dawg
Goddamnit.
It took me up until reading your comment to get this one. "Is it that the scaling transformation only scaled the y-axis?? Oh..."
I teach these basic transformations as part of my middle school math classes, and I was completely loss as to why they didn't include a reflection, but then I realized a reflection wouldn't be that interesting because it could be indistinguishable from a translation.
I was at a loss too as to where they source the "most common" when skewing is also extremely common
Scaling, in general, is the least common middle school transformation covered by state curriculum as far as depth of knowledge is concerned, at least where I've taught. Students just aren't ready at that age to calculate something as sophisticated as the scale factor contributing to an object's loss of size.
I think the students are ready and quite capable of such sophistication. They're just too distracted with sharing memes.
I think the students are ready and quite capable of such sophistication. They're just too distracted with sharing memes.
(Oh, I know, my middle schoolers do alright as long as our figures are two-dimensional, and my high school geometry students do very well; I just wanted to say the magic, fun, wink wink word again. 🙂)