this post was submitted on 27 Feb 2024
7 points (100.0% liked)

Science Memes

11004 readers
3123 users here now

Welcome to c/science_memes @ Mander.xyz!

A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.

Rules

  1. Don't throw mud. Behave like an intellectual and remember the human.
  2. Keep it rooted (on topic).
  3. No spam.
  4. Infographics welcome, get schooled.

This is a science community. We use the Dawkins definition of meme.

Research Committee

Other Mander Communities

Science and Research

Biology and Life Sciences

Physical Sciences

Humanities and Social Sciences

Practical and Applied Sciences

Memes

Miscellaneous

founded 2 years ago
MODERATORS
[email protected]
[email protected]
[email protected]
7
hmmmm (mander.xyz)
submitted 8 months ago by [email protected] to c/[email protected]
192 comments fedilink hide all child comments
 
you are viewing a single comment's thread
view the rest of the comments
[–] [email protected] 0 points 8 months ago* (last edited 8 months ago) (1 children)

Infinity cannot be divided, if it can then it becomes multiple finite objects.

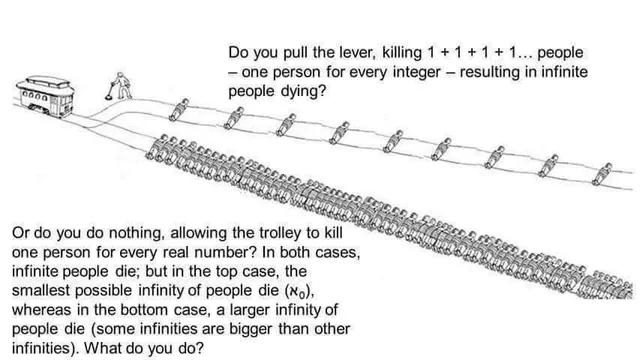
It really depends on what you mean by infinity and division here. The ordinals admit some weaker forms of the division algorithm within ordinal arithmetic (in particular note the part about left division in the link). In fact, even the cardinals have a form of trivial division.

Additionally, infinite sets can often be divided into set theoretic unions of infinite sets fairly easily. For example, the integers (an infinite set) is the union of the set of all integers less than 0 with the set of all integers greater than or equal to 0 (both of these sets are of course infinite). Even in the reals you can divide an arbitrary interval (which is an infinite set in the cardinality sense) into two infinite sets. For example [0,1]=[0,1/2]U[1/2,1].

Therefore there cannot be multiple Infinities.

In the cardinality sense this is objectively untrue by Cantor's theorem or by considering Cantor's diagonal argument.

Edit: Realized the other commenter pointed out the diagonal argument to you very nicely also. Sorry for retreading the same stuff here.

Within other areas of math we occasionally deal positive and negative infinities that are distinct in certain extensions of the real numbers also.

If infinity has a size, then it is a finite object.

Again, this is not really true with cardinals as cardinals are in some sense a way to assign sizes to sets.

If you mean in terms of senses of distances between points, in the previous link involving the extended reals, there is a section pointing out that the extended reals are metrizable, informally this means we can define a function (called a metric) that measures distances between points in the extended reals that works roughly as we'd expect (such a function is necessarily well defined if either one or both points are positive or negative infinity).

[–] [email protected] 0 points 8 months ago (1 children)

If infinity can be measured, by either size, shape, distance, timespan or lifecycle, then the object being considered infinite is a finite object. Infinity, nothing, and everything follow these same rules. If there are two multiple infinite objects side by side to each other, which means there is a measurable boundry that seperates them, then those objects aren't infinite, they are finite objects, within an infinite space that contains them. Only the space that contains these objects is infinite. Any infinite numbers that are generated within this infinite space, regardless of where they originated within this space, belong to this single infinity. There is no infinityA or infinityB there is just infinity itself.

[–] [email protected] 0 points 8 months ago* (last edited 8 months ago) (1 children)

My degree is in math. I feel pretty confident in saying that you are tossing around a whole bunch of words without actually knowing what they mean in a mathematical context.

If you disagree, try the following:

  1. What is a function? What is an injective function? What is a surjective function? What is a bijection?

  2. In mathematics, what does it mean for a set to be finite?

  3. In mathematics, what does it mean for a set to be infinite?

I'm willing to continue this conversation if you can explain to me in reasonably rigorous terms what those words mean. I'll help you do it too. The link I sent you in my previous post that mentions cardinal numbers links you to a wikipedia page that links to articles explaining what finite and infinite sets are in the first paragraph.

To be clear here, your answer for 2 specifically should rely on your answer from 1 as the mathematical definition of a finite set is in terms of functions and bijections.

Here are some bonus questions for you to try also:

  1. In mathematics, what does it mean for a set to be countable?

  2. In mathematics, what does it mean for a set to be uncountable?

[–] [email protected] 0 points 8 months ago (1 children)

A finite universe, the one in which we live, can only produce finite objects. Those finite objects can only produce other finite objects. A finite object cannot create an infinite object, as the act of creation would be a starting point for the object, and if an object has a starting point or an end point, which are really the same thing, then the object is a finite object.

If a set of numbers originates from a starting point and moves away from that point in a seemingly infinite distance, and then you decide to traverse that set in the opposite direction towards the starting point, the starting point becomes an ending point, and if an object, in this case the set itself, has an ending point, it is a finite object. Finite objects cannot create infinite objects because the act of creation would negate their infinity. Infinity is neither created nor ends, nor does it have size, shape, or form.

[–] [email protected] 0 points 8 months ago* (last edited 8 months ago) (1 children)

None of this includes the correct answers to the questions I asked you. I'm not going to read anything else from you until you correctly answer the questions I asked.

[–] [email protected] 0 points 8 months ago (1 children)

I find it interesting that you have a degree in math, and apparently have never questioned a question. As I've demonstrated, in the posted problem, the statement "some Infinities are bigger than other infinities" is an illogical statement. The mere statement that there are multiple infinities, negates either objects identification as being infinite, and reduces both objects to finite objects, as the only way these objects can be determined to be seperate from each other is through a boundary that would impose a starting or ending point on each object, which in turn reduces them into finite objects.

I also find it interesting that you resort to gate keeping to try and control a situation that you are frustrated by. I was able to simply and clearly demonstrate my position. I also demonstrated the technique of: solving the problem by defeating its purpose. I've also demonstrated the difference in how a mathematician and an engineer attempt to solve a problem.

[–] [email protected] 0 points 8 months ago (1 children)

To me you have demonstrated:

  1. You don't know even the most basic definitions of the things you are trying to talk about.

  2. You are possibly too willfully stupid to bother to learn said definitions.

  3. You are capable of babbling incoherently about things you do not understand ad nauseum.

[–] [email protected] 0 points 8 months ago (1 children)

It seems you are having a hard time comprehending this. I get it's hard to learn new things. But I can walk you through it.

TL;DR: If an object can be measured, in any way, it's a finite object. Infinity cannot be measured.

  1. In the posted problem the train tracks themselves are finite objects, as they each have a starting point, the fork the train is in front of.
  2. The train tracks are bound to physical ground, ground that is itself bound to a finite world, a world has a shape, that can be measured, so it is a finite object.
  3. If the shape of the world the train tracks are on is round, then these seemingly infinite tracks will eventually loop back on themselves. If the tracks loop back on themselves, then they must eventually converge as the train starts out the problem on a single track. So neither of the tracks are infinite.
  4. It's important to understand that the tracks are finite objects, as finite objects exist by different rules then infinity itself.
  5. I'm not arguing that uncountable numbers are a thing. What I am stating is that if those numbers exist within a finite universe, then they have a lifespan, the lifespan of the finite universe that contains them, thus those numbers aren't infinite, uncountable yes, but not truly infinite. As I have stated many times, finite objects, like the finite universe, can only create other finite objects. Infinity cannot be created, therefore there is only one infinity, infinity itself, all other objects that can be measured are finite objects. This also means if infinity decides to create anything, it can only produce finite objects. Infinity cannot produce another infinity, as the act of creation would be a measurable starting point.
  6. This is why the statement (some infinities are smaller than other infinities) is an illogical statement. If you can measure multiple infinities, then none of those objects are infinite, as one object can be measured to be smaller or larger than the other. And as I keep stating, infinity cannot be measured. If your measurement is uncountable, then the measurement itself is finite.
[–] [email protected] 0 points 8 months ago* (last edited 8 months ago) (1 children)

I considered reading and responding to this big long word salad you sent me, but I realized you were just further demonstrating the three points from my last post. Lmao, good luck.

Edit: Feel free to show me you learned the definitions I asked you about by answering my list of definition questions I posed to you a while ago by the way. I'm still fine with continuing if you do that.

[–] [email protected] 0 points 8 months ago (1 children)

I get it it's hard to learn new things. I'm still willing to walk you through it. I'm not sure how much more simple I can state it for you, it's already pretty simplified, but I'm still willing to try. Just let me know.

[–] [email protected] 0 points 8 months ago (1 children)

I understand that you feel learning new things is hard. I sympathize with you. Lets start with a real easy one. High school algebra students often learn what mathematical functions are. You can handle that right? Tell me the mathematical definition of a function. Oh! Oops, I have accidentally linked you to a place where you can find the definition I'm asking you for in the first paragraph. Well, no going back now. Feel free to copy and paste the first paragraph of that link here.

Hmm, I wonder if there is a link between functions and finite/infinite sets? Oh gosh golly, perhaps they are related in some way? Almost like the definition of one requires some notion of the other?

[–] [email protected] 0 points 8 months ago

I've never argued that mathematics has a concept of finite or infinite numbers, or not. All that I have argued is that what the math world identifies as infinite, is not actually infinite when applied to the real world. As an engineer I deal with recursive functions, code that can run indefinitely. But as an engineer I understand that the code that is running needs an initiation point, the point at which the code is initially executed, and I understand that the seemingly infinite nature of the code, is bound to the lifespan of the process that execute it, for example, until the process is abruptly stopped, or power is taken away from the computer the process is running on. A lifespan invalidates the seemingly infinite nature of the code, from a practical sense. When you start to understand this, and then expand your focus to larger objects like the universe itself, you start to understand the finite nature of the material world we live in.

I understand that mathematicians deal with abstraction. I deal with them too as an engineer. The difference is that as an engineer I have to implement those abstractions within the real world. When you do this enough times you will start to understand the stark differences between the limited hypothetical worlds math is reasoned about, and the very dynamic world the real world, that those math solutions are applied to. The rules of hypothetical worlds are severely limited in comparison to the real world. This is why it's very important for me to define the real world boundaries that these math problems wil be applied to.

I'm used to working with folks, like yourself, that have a clearly hard time transitioning from a hypothetical world to the real world. This is why I have respond with civility, and have looked past your responses insulting tone. I understand it's a fear response of the ego, and I don't judge you for it. I understand that it's difficult to fight with the protection mechanisms of the ego.