this post was submitted on 08 Oct 2024
1121 points (98.3% liked)
People Twitter
6985 readers
1181 users here now
People tweeting stuff. We allow tweets from anyone.
RULES:
- Mark NSFW content.
- No doxxing people.
- Must be a pic of the tweet or similar. No direct links to the tweet.
- No bullying or international politcs
- Be excellent to each other.
- Provide an archived link to the tweet (or similar) being shown if it's a major figure or a politician.
founded 2 years ago
MODERATORS
you are viewing a single comment's thread
view the rest of the comments
view the rest of the comments
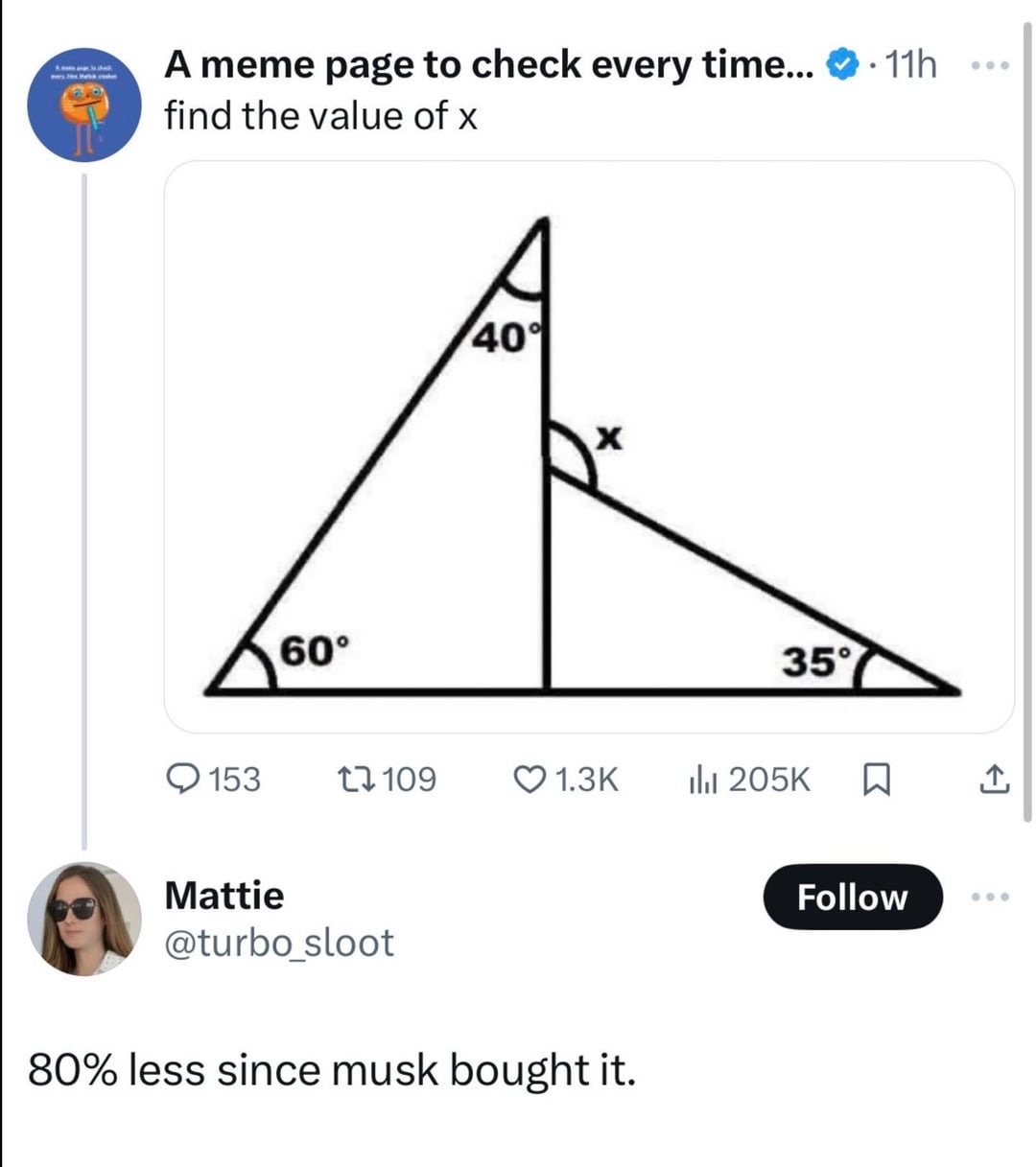
Why do the labeled angles prevent us from assuming straight lines?
Because the apparently straight lines contradict the labels. As drawn, the unlabeled bottom vertices are clearly 90°, not 80° and 100°. We must either conclude that the labels are incorrect, or that the figure is not drawn to scale. Either way, it's insoluble.
Because the angles aren't represented accurately. It could be that the two angles that look like they're 90° add up to 180°, but they could also not
That's technically possible, but that's also an irrational take. The rational take is to assume the problem is solvable given the available information, which means assuming that the lines are straight.
Yes, two angles appear to be 90⁰, but they're obviously not with the given information. Math conventions nearly always label right angles, so not having the right angle there implies that the angle should not be assumed to be 90⁰. Math conventions in trigonometry also generally assume straight lines unless there's a visual indicator that they're not, and those tend to be exaggerated so it's obvious.
So the rational answer here is that the bottom line is straight and therefore the problem is solvable. Saying otherwise is irrational, because that's so far away from math conventions.