this post was submitted on 30 Oct 2024

392 points (97.6% liked)

Science Memes

11021 readers

4040 users here now

Welcome to c/science_memes @ Mander.xyz!

A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.

Rules

Don't throw mud. Behave like an intellectual and remember the human.
Keep it rooted (on topic).
No spam.
Infographics welcome, get schooled.

This is a science community. We use the Dawkins definition of meme.

Research Committee

[email protected]

Other Mander Communities

Science and Research

Biology and Life Sciences

Physical Sciences

Humanities and Social Sciences

Practical and Applied Sciences

Memes

Miscellaneous

founded 2 years ago

MODERATORS

[email protected]

392

This feels wrong. I love it. (sopuli.xyz)

submitted 2 weeks ago by [email protected] to c/[email protected]

67 comments fedilink hide all child comments

you are viewing a single comment's thread
view the rest of the comments

[+] [email protected] 11 points 2 weeks ago (3 children)

[deleted]

[–] [email protected] 11 points 2 weeks ago (1 children)

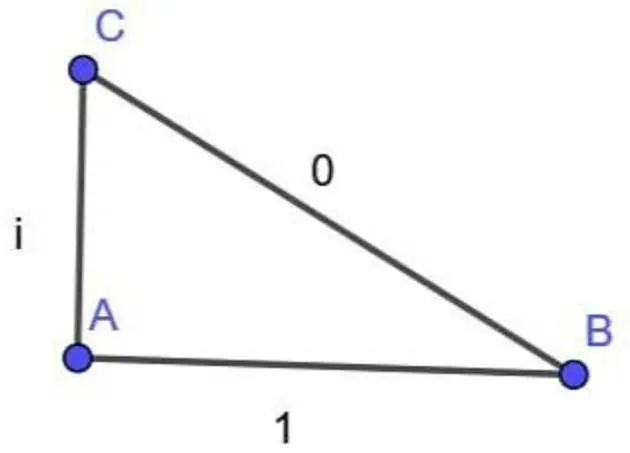
If AB = i and BC = 0, then B would be in the same 2D space as C, but one of them would be "above" the other in 3D space (which doesn't exist in this context, just as sqrt(-1) doesn't exist in the traditional sense).

So this triangle represents a 2D object that is "standing up" on the page.

[–] [email protected] 7 points 2 weeks ago* (last edited 2 weeks ago) (1 children)

It makes sense if you represent complex numbers as (a, b) pairs, where a is the real part and b is the imaginary part (just like the popular a + bi representation that can be expanded to a * (1, 0) + b * (0, 1)). AB's length is (1, 0), AC's length is (0, 1), and BC's length will also be a complex number.

I think.

[–] [email protected] 1 points 2 weeks ago

Yes. Also if you think of i as a 90° rotation (with a length of the scalar coefficient infront of i, in this case 1) . Thus one rotates you outwards away from the 2D plane, and two of those gets you back to the 2D plane, just going the other direction.

[–] [email protected] 31 points 2 weeks ago (2 children)

The reason it doesn't work is that 1 is a scalar while i is a vector (with magnitude 1). The Pythagoras theorem works with scalars, not vectors, so you'd get 1^2 +1^2 = 2.

[–] [email protected] 6 points 2 weeks ago

I am sorry, but.. to be pedantic, pythagorean theorem works on real-valued length. Complex numbers can be scalars, but one does not use it for length for some reason I forgor.

[–] [email protected] 7 points 2 weeks ago* (last edited 2 weeks ago) (1 children)

Far as I understand it (which is not very far), i is a scalar even if you take it to be the complex number 0 + i. Just by itself i is the imaginary unit that's defined as i = sqrt(-1) (edit: or, well, the solution to x² + 1 = 0, but same difference), and nothing in that definition says it's a vector quantity.

Even though complex numbers do extend real numbers into a 2D plane doesn't mean they're automatically vectors, and – again, as far as I've understood things – they're still treated as single entities, ie. scalars. i by itself isn't a complex number I think, though.

The joke is that i² = -1 by definition, so i² + 1² = 0²

Edit: eg. nothing on the imaginary number wiki page implies that the imaginary unit is not a scalar value

[–] [email protected] 6 points 2 weeks ago (1 children)

whether or not i is a scalar depends entirely on the context.

every vector space has an associated field of coefficients. in practice, this field is typically the real numbers. but you can have lots of other kinds of vector spaces as well, and they can be useful for certain things.

anyways, if you have a vector space over the complex numbers, then i is a scalar, because it is a complex number. if you have a vector space over the real numbers, then i is not a scalar, because it’s not a real number.

its worth mentioning that you can view the complex numbers as a vector space over itself. this is just a fancy way of saying that you can add complex numbers together, and you can multiply a complex number by a complex number. (one of those numbers is playing the role of scalar, and the other is playing the role of vector.) but you can also view the complex numbers as a vector space over the real numbers. and this is just a fancy way of saying that you can add complex numbers, and you can multiply a complex number by a real number.

[–] [email protected] 2 points 2 weeks ago (1 children)

Right, sort of my vague understanding as well although it's been 15 years since my university math courses. My point was more that "1 is a scalar while i is a vector" just didn't seem correct to me, at least on a general level

[–] [email protected] 2 points 2 weeks ago

ah true. i missed the context of the original comment since it got deleted, but you're completely right that the “1 is a scalar while i is a vector” statement is not entirely accurate.

[–] [email protected] 2 points 2 weeks ago

A?= 90°