Science Memes

10940 readers

1968 users here now

Welcome to c/science_memes @ Mander.xyz!

A place for majestic STEMLORD peacocking, as well as memes about the realities of working in a lab.

Rules

Don't throw mud. Behave like an intellectual and remember the human.
Keep it rooted (on topic).
No spam.
Infographics welcome, get schooled.

This is a science community. We use the Dawkins definition of meme.

Research Committee

[email protected]

Other Mander Communities

Science and Research

Biology and Life Sciences

Physical Sciences

Humanities and Social Sciences

Practical and Applied Sciences

Memes

Miscellaneous

founded 2 years ago

MODERATORS

[email protected]

372

Conversing with Mathematicians (mander.xyz)

submitted 3 months ago by [email protected] to c/[email protected]

57 comments fedilink hide all child comments

you are viewing a single comment's thread
view the rest of the comments

[–] [email protected] 2 points 3 months ago (1 children)

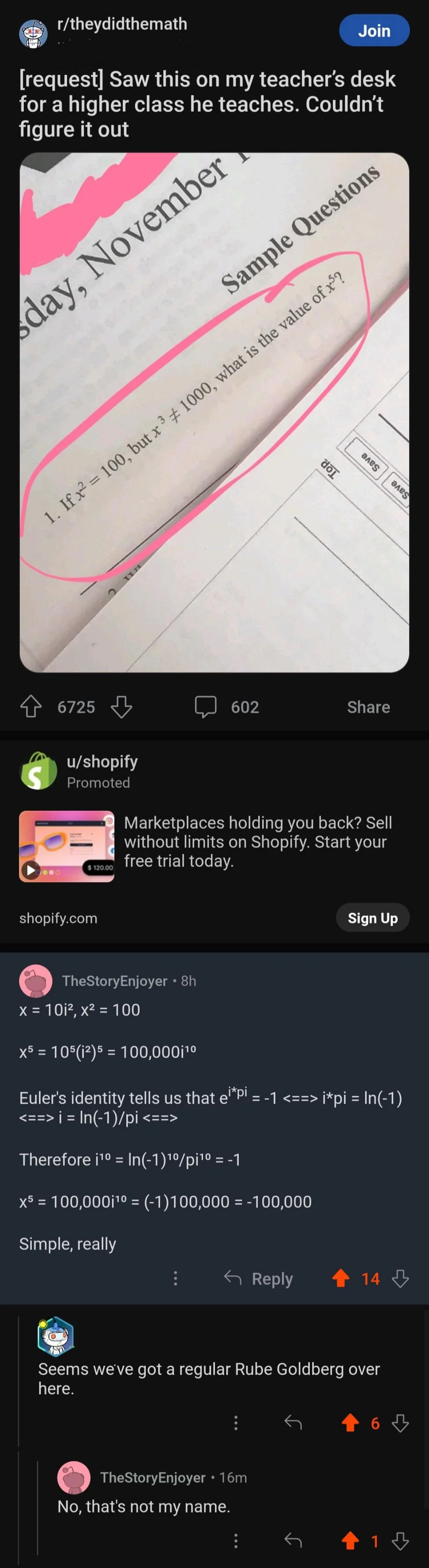
If we know the values of ln(-1)¹⁰ and pi¹⁰ we hypothetically could calculate their divided result as -1 instead of using strict logic, but it is missing a few steps. Moreover logs of negative numbers just end up with an imaginary component anyway so there isn't really any progress to be made on that front. Typing ln(-1)¹⁰ into my scientific calculator just yields i¹⁰pi¹⁰, (I'm guessing stored rather than calculated? Maybe calculated with built in Euler) so the result of division is just i¹⁰ anyway and we're back where we started.

[–] [email protected] 2 points 3 months ago

You can find the value of ln(-1)¹⁰ by examining the definition of ln(x): the result z satisfies eᶻ=x. For x=-1, that means the z that satisfies eᶻ=-1. Then we know z from euler's identity. Raise to the 10, and there's our answer. And like you pointed out, it's not a particularly helpful answer.