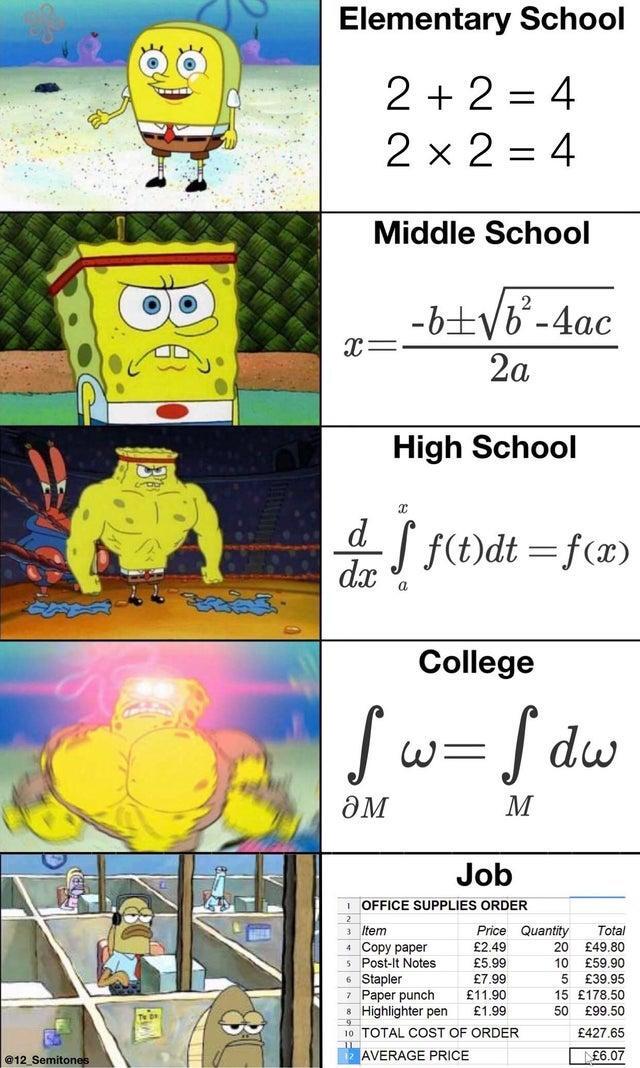Memes
Rules:
- Be civil and nice.
- Try not to excessively repost, as a rule of thumb, wait at least 2 months to do it if you have to.
We did a lot of straight algebra in highschool, I don't need the exact skill but its boosted my abstract thinking a lot which helps in other things
Lucky, my school only did gay algebra and look at me now 😩
But have you found x 😁
Most of the math I do at work is related to compound interest. Of all the math I believe the general public should understand, the concept of how paying interest to others is a total screw would get my top vote.
I have a co-worker who took out a car loan last week at, wait for it, FIFTY THREE PERCENT INTEREST! No concept of what that was costing her. She could only see, "I can afford the monthly payment."
(1 + r)^n and its friend 1/(1 + r)^n have been the two most important concepts in work and personal life that I've ever learned and applied.
That is usury. That cannot be legal? Oh, no, I just checked, wow, usury laws are weak af.
Usury was indeed the term that immediately came to mind.
53%?!
Sounds like one of those shitty used car joints “no credit, no problem” that you sign your life away for a mediocre car.
Sounds like predatory lending
I would agree, but it's not my life, not my money. You can't really go around telling people they fucked up every time you see it.
True. Plus, while dumb, 53% will always beat the interest extracted by two goons and a baseball bat. There's always a trade-off!
How the hell is "average price" useful?
Thats like buying potatoes and pork chops and saying the average price is $8.75. Technically true but practically useless.
What's the college one mean?
It's the most general form of Stokes' theorem that the integral of a differential form over the boundary of an volume and the integral of an exterior derivative of this form over that volume are the same. It covers a lot of classic formulas from the fundamental theorem of calculus to Green's theorem, Gauss' theorem and classic Stokes' theorem.
Same as high school but fancier?
Stokes' theorem. Almost the same thing as the high school one. It generalizes the fundamental theorem of calculus to arbitrary smooth manifolds. In the case that M is the interval [a, x] and ω is the differential 1-form f(t)dt on M, one has dω = f'(t)dt and ∂M is the oriented tuple {+x, -a}. Integrating f(t)dt over a finite set of oriented points is the same as evaluating at each point and summing, with negatively-oriented points getting a negative sign. Then Stokes' theorem as written says that f(x) - f(a) = integral from a to x of f'(t) dt.
Almost the same thing 😏